
Vectors:
A Curriculum Module
for AP
®
Calculus BC
2010
Curriculum Module
The College Board
e College Board is a not-for-prot membership association whose mission is to
connect students to college success and opportunity. Founded in 1900, the College Board
is composed of more than 5,700 schools, colleges, universities and other educational
organizations. Each year, the College Board serves seven million students and their
parents, 23,000 high schools, and 3,800 colleges through major programs and services in
college readiness, college admission, guidance, assessment, nancial aid and enrollment.
Among its widely recognized programs are the SAT®, the PSAT/NMSQT®, the Advanced
Placement Program® (AP®), SpringBoard® and ACCUPLACER®. e College Board is
committed to the principles of excellence and equity, and that commitment is embodied
in all of its programs, services, activities and concerns.
For further information, visit www.collegeboard.com.
e College Board wishes to acknowledge all the third-party sources and content that
have been included in these materials. Sources not included in the captions or body of
the text are listed here. We have made every eort to identify each source and to trace the
copyright holders of all materials. However, if we have incorrectly attributed a source or
overlooked a publisher, please contact us and we will make the necessary corrections.
© 2010 e College Board. College Board, ACCUPLACER, Advanced Placement
Program, AP, AP Central, Pre-AP, SpringBoard and the acorn logo are registered
trademarks of the College Board. inspiring minds is a trademark owned by the College
Board. PSAT/NMSQT is a registered trademark of the College Board and National Merit
Scholarship Corporation. All other products and services may be trademarks of their
respective owners. Visit the College Board on the Web: www.collegeboard.com.
Contents
Introduction ........................................................................................... 4
Day 1: Graphing Parametric Equations and Eliminating
the Parameter .......................................................................... 6
Day 2: Parametric Equations and Calculus ................................ 14
Day 3: Review of Motion Along a Line ........................................ 22
Day 4: Motion Along a Curve — Vectors .................................... 27
Day 5: Motion Along a Curve — Vectors (continued) ............. 35
Day 6: Motion Along a Curve — Vectors (continued) ............. 39
About the Author ................................................................................ 43

© 2010 e College Board.
4
Vectors
Vectors in AP
®
Calculus BC
Nancy Stephenson
Clements High School
Sugar Land, Texas
Introduction
According to the AP® Calculus BC Course Description, students in Calculus BC are
required to know:
• Analysis of planar curves given in parametric form and vector form, including
velocity and acceleration vectors
• Derivatives of parametric and vector functions
• e length of a curve, including a curve given in parametric form
What does this mean? For parametric equations
x f t=
( )
and
y g t=
( )
, students
should be able to:
1. Sketch the curve dened by the parametric equations and eliminate the parameter.
2. Find
dy
dx
d y
dx
and
2
2
and
dy
dx
d y
dx
and
2
2
and evaluate them for a given value of t.
3. Write an equation for the tangent line to the curve for a given value of t.
4. Find the points of horizontal and vertical tangency.
5. Find the length of an arc of a curve given by parametric equations.
For vectors describing particle motion along a curve in terms of a time variable t,
students should be able to:
1. Find the velocity and acceleration vectors when given the position vector.
2. Given the components of the velocity vector and the position of the particle at a
particular value of t, nd the position at another value of t.
3. Given the components of the acceleration vector and the velocity of the particle at
a particular value of t, nd the velocity at another value of t.
4. Find the slope of the path of the particle for a given value of t.
5. Write an equation for the tangent line to the curve for a given value of t.
6. Find the values of t at which the line tangent to the path of the particle is
horizontal or vertical.

© 2010 e College Board.
5
Vectors
7. Find the speed of the particle (sometimes asked as the magnitude of the velocity
vector) at a given value of t.
8. Find the distance traveled by the particle for a given interval of time.
I like to start this unit with parametric equations, teaching the students the ve
types of parametric problems listed above. en I take a day to review the concept of
motion along a horizontal or vertical line, which they learned earlier in the year, as a
bridge to motion along a curve.
e unit on parametric equations and vectors takes me six days to cover (see the
following schedule), not including a test day. I teach on a traditional seven-period day,
with 50 minutes in each class period.
Day 1 — Graphing parametric equations and eliminating the parameter
Day 2 — Calculus of parametric equations: Finding
dy
dx
d y
dx
and
2
2
and
dy
dx
d y
dx
and
2
2
and
evaluating them for a given value of t, nding points of horizontal and
vertical tangency, nding the length of an arc of a curve
Day 3 — Review of motion along a horizontal and vertical line. (e students
have studied this topic earlier in the year.)
Days 4, 5 and 6 — Particle motion along a curve (vectors):
• Finding the velocity and acceleration vectors when given the position vector;
• Given the components of the velocity vector and the position of the particle at one
value of t, nding the position of the particle at a dierent value of t;
• Finding the slope of the path of the particle for a given value of t;
• Writing an equation for the tangent line to the curve for a given value of t;
• Finding the values of t at which the line tangent to the path of the particle
is horizontal or vertical;
• Finding the speed of the particle; and
• Finding the distance traveled by the particle for a given interval of time.
© 2010 e College Board.
6
Vectors
Day 1: Graphing Parametric
Equations and Eliminating
the Parameter
My students have studied parametric equations and vectors in their precalculus course, so
this lesson is a review for them. Many of them have also studied parametric equations and
vectors in their physics course. If your textbook contains this material, you might want to
follow your book here.
Directions: Make a table of values and sketch the curve, indicating the direction of your
graph. en eliminate the parameter.
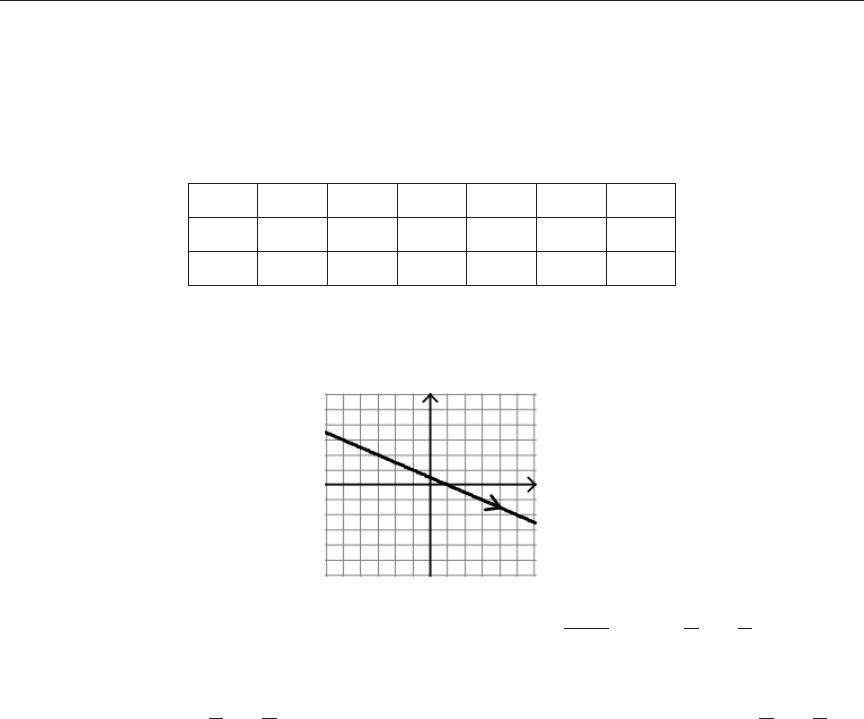
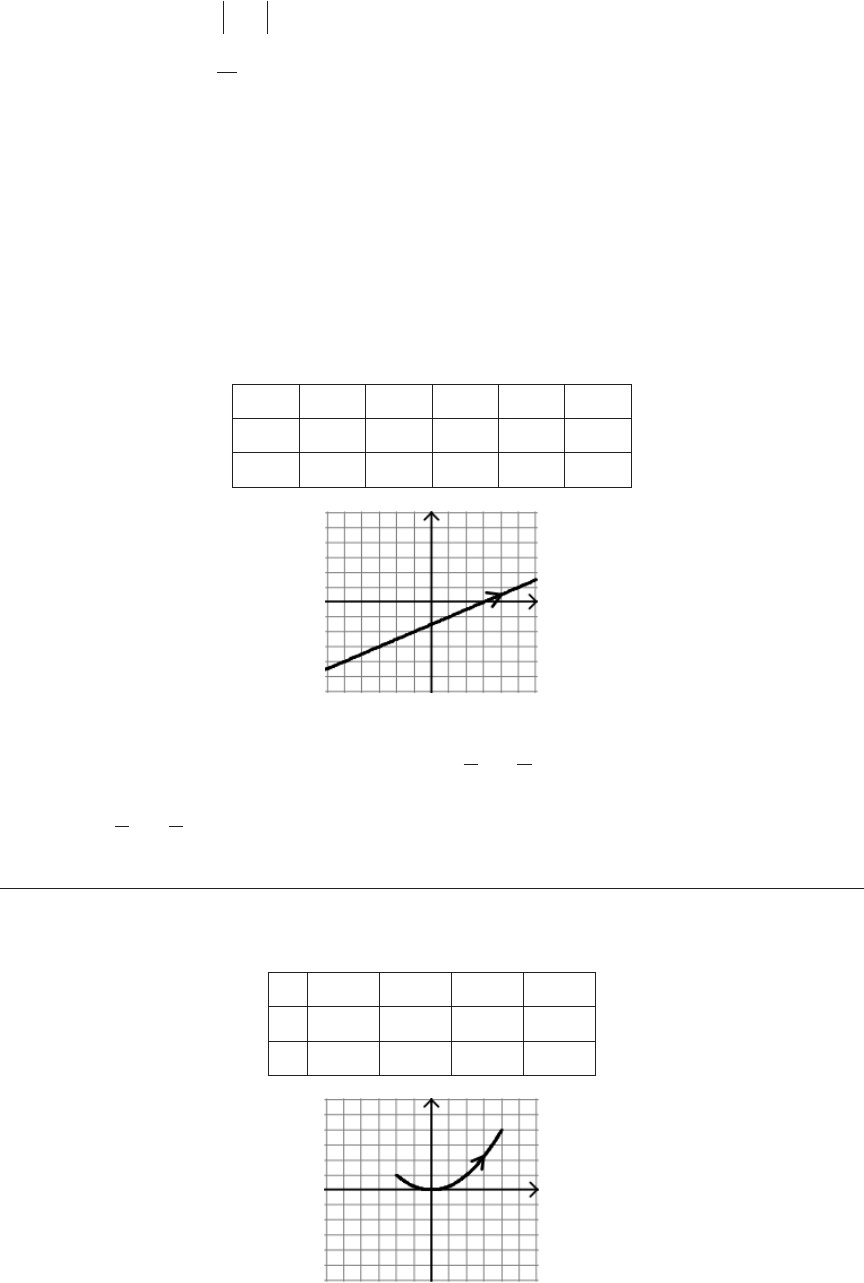
(a)
x t y t= − = −2 1 1 and
Solution: First make a table using various values of t, including negative numbers,
positive numbers and zero, and determine the x and y values that correspond to
these t values.
t
–2 –1 0 1 2 3
x
–5 –3 –1 1 3 5
y
3 2 1 0 –1 –2
Plot the ordered pairs
x y,
( )
, drawing an arrow on the graph to indicate its
direction as t increases.
To eliminate the parameter, solve
x t= −2 1
for
t
x
t x=
+
= +
1
2
1
2
1
2
or .
en
substitute
t x= +
1
2
1
2
in place of t in the equation y = 1 – t to get
y x= − +
1
2
1
2
.
Look at the graph of the parametric equations to see if this equation matches the
graph, and observe that it does.
© 2010 e College Board.
7
Vectors
(b)
x t y t= = +, 1
Solution: Since
x t=
, we can use only nonnegative values for t.
t
0 1 4 9
x
0 1 2 3
y
1 2 5 10
To eliminate the parameter, solve
x t t x= = for
2
. en substitute
t x=
2
into
y’s equation so that
y x= +
2
1
. To make this equation match the graph, we must
restrict x so that it is greater than or equal to 0. e solution is
y x x= + ≥
2
1 0,
.
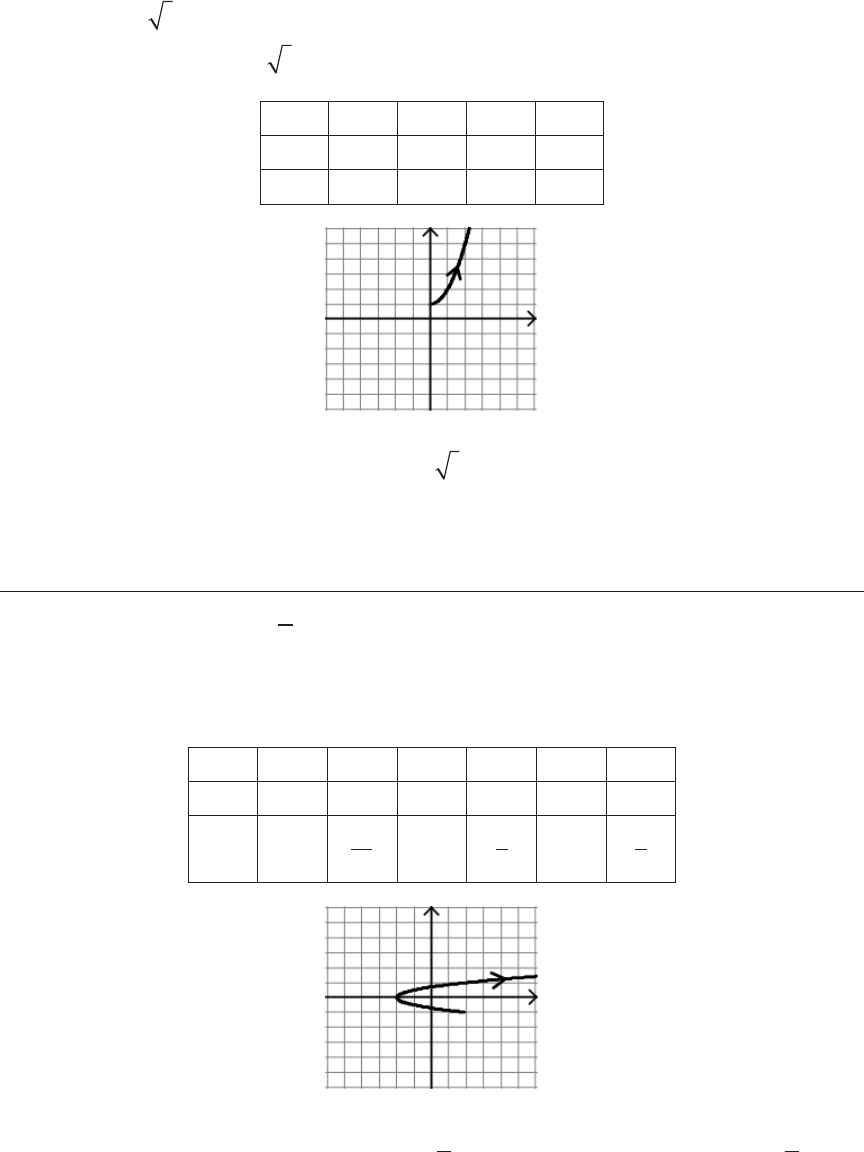
(c) x = t
2
– 2 and y =
t
2
, –2 ≤ t ≤ 3
Solution: First make a table using t values that lie between –2 and 3, and
determine the x and y values that correspond to these t values.
t
–2 –1 0 1 2 3
x
2 –1 –2 –1 2 7
y
–1
−1
2
0
1
2
1
3
2
To eliminate the parameter, solve
y
t
=
2
for t to nd that
t y= 2
,
− ≤ ≤1
3
2
y
. en
substitute 2y in place of t in the other equation so that
x y
= −4 2
2
. To make this
© 2010 e College Board.
8
Vectors
equation match the graph, we must restrict y so that it lies between
−1
3
2
and
. e
solution is
x y y= − − ≤ ≤4 2 1
3
2
2
,
.
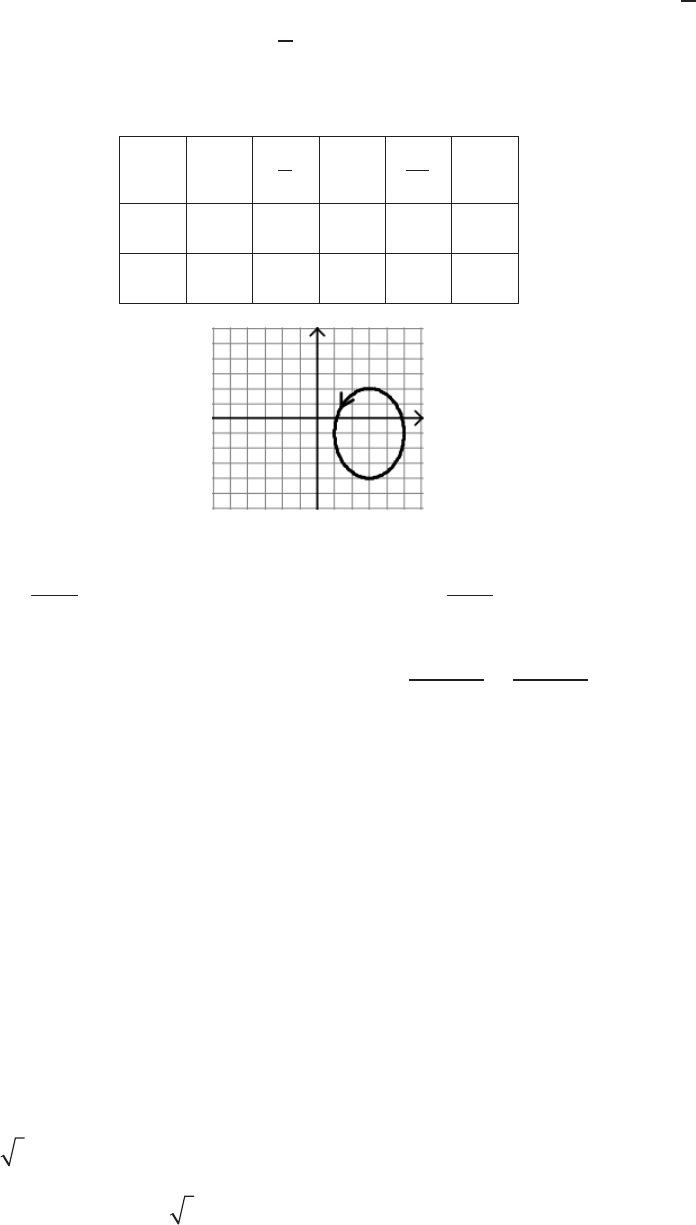
(d)
x t y t= + = − +3 2 1 3cos , sin
t
0
π
2
π
3
2
π
2
π
x
5 3 1 3 5
y
–1 2 –1 –4 –1
Solution: To eliminate the parameter, solve for
cos t
in x’s equation to get
cos t
x
=
− 3
2
and
sin t
in y’s equation to get
sin t
y
=
+1
3
. Substitute into the
trigonometric identity
cos sin
2 2
1t t+ =
to get
x y−
( )
+
+
( )
=
3
4
1
9
1
2 2
. Discuss
with the students the fact that this is an ellipse centered at the point (3, –1) with a
horizontal axis of length 4 and a vertical axis of length 6.
Day 1 Homework
Make a table of values and sketch the curve, indicating the direction of your graph. en
eliminate the parameter. Do not use your calculator.
1.
x t y t= + = −2 1 1 and
2.
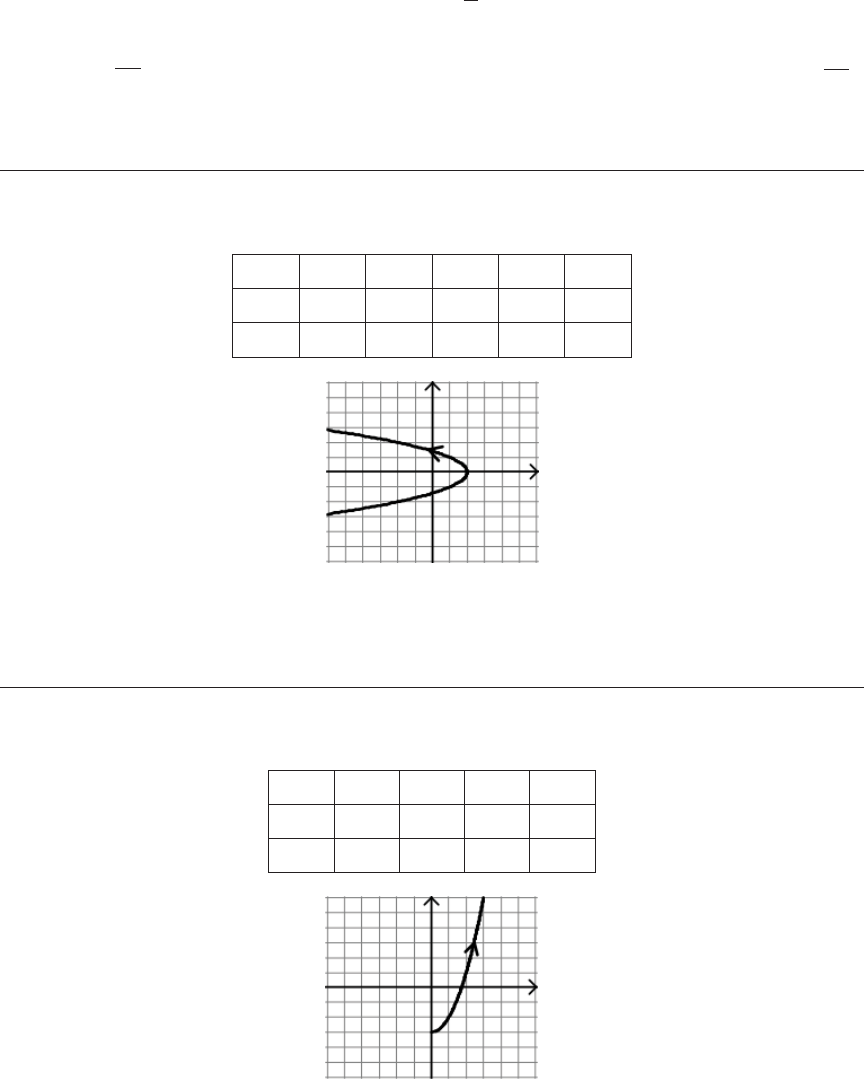
x t y t t= = − ≤ ≤2 1 2
2
and ,
3.
x t y t= − =2
2
and
4.
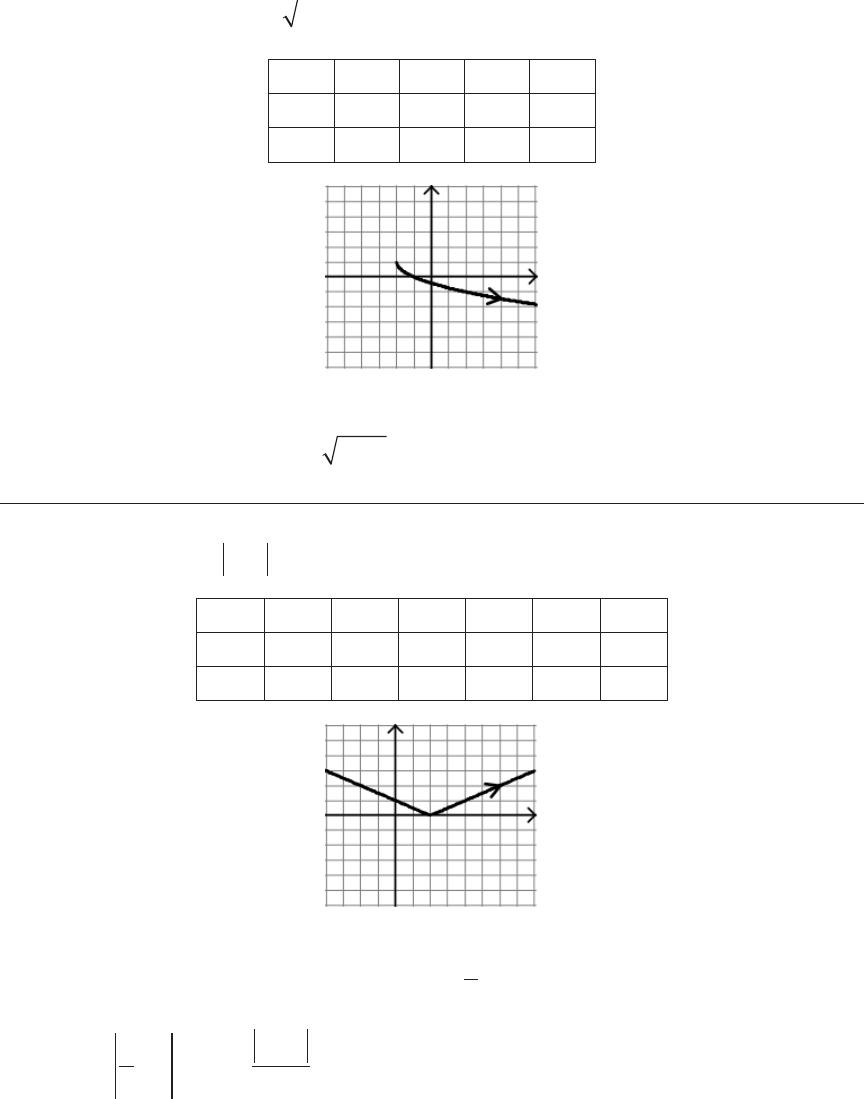
x t y t= = − and 3
5.
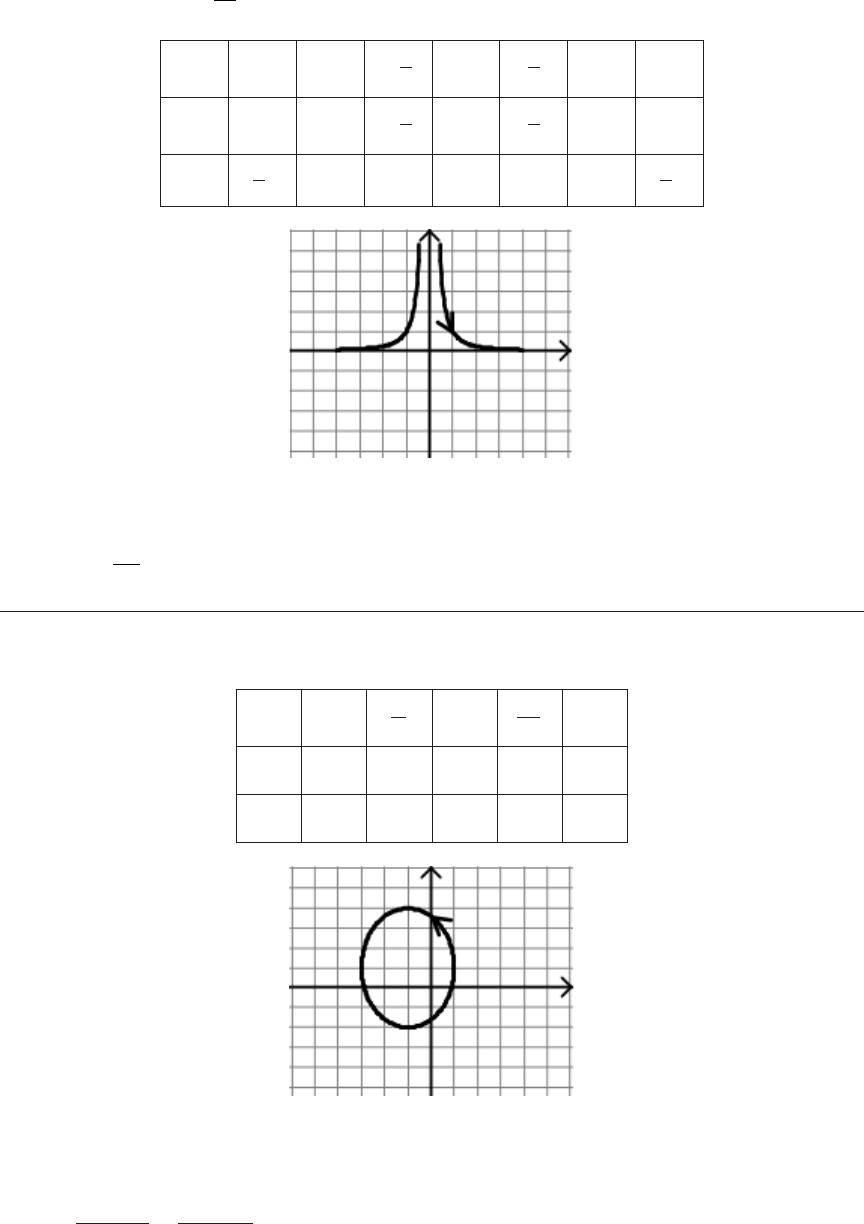
x t y t= − = −2 1 and
© 2010 e College Board.
9
Vectors
6.
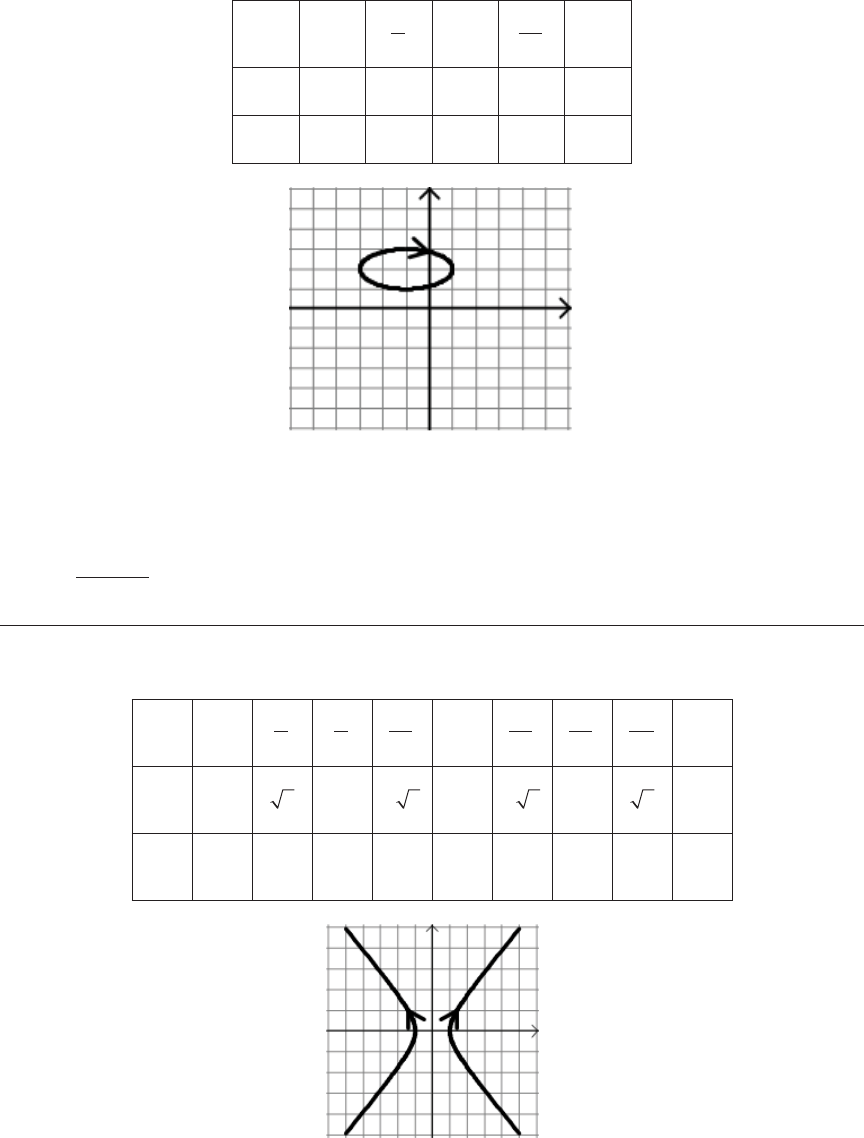
x t y t= = −2 1 and
7.
x t y
t
= = and
1
2
8.
x t y t= − = +2 1 3 1cos sin and
9.
x t y t= − = +2 1 2sin cos and
10.
x t y t= =sec tan and
Answers to Day 1 Homework
1.
x t y t= + = −2 1 1 and
t
–2 –1 0 1 2
x
–3 –1 1 3 5
y
–3 –2 –1 0 1
To eliminate the parameter, solve for
t x= −
1
2
1
2
. Substitute into y’s equation to get
y x= −
1
2
3
2
.
2.
x t y t t
= = − ≤ ≤2 1 2
2
and ,
t
–1 0 1 2
x
–2 0 2 4
y
1 0 1 4
© 2010 e College Board.
10
Vectors
To eliminate the parameter, solve for
t
x
=
2
. Substitute into y’s equation to get
y
x
x= − ≤ ≤
2
4
2 4,
. (Note: e restriction on x is needed for the graph of
y
x
=
2
4
to match the parametric graph.)
3.
x t y t= − =2
2
and
t
–2 –1 0 1 2
x
–2 1 2 1 –2
y
–2 –1 0 1 2
To eliminate the parameter, notice that t = y. Substitute into x’s equation to get
x y= −2
2
.
4.
x t y t= − = −2 3
2
and
t
0 1 4 9
x
0 1 2 3
y
–3 –2 1 6
To eliminate the parameter, solve for t = x
2
. Substitute into y’s equation to get y = x
2
– 3, ≥ 0. (Note: e restriction on x is needed for the graph of y = x
2
– 3 to match
the parametric graph.)
© 2010 e College Board.
11
Vectors
5.
x t y t= − = −2 1 and
t
0 1 4 9
x
–2 –1 2 7
y
1 0 –1 –2
To eliminate the parameter, solve for
t x x= + ≥ −2 2,
(since
t ≥ 0
). Substitute into
y’s equation to get
y x= − +1 2
.
6.
x t y t= = −2 1 and
t
–2 –1 0 1 2 3
x
–4 –2 0 2 4 6
y
3 2 1 0 1 2
To eliminate the parameter, solve for
t
x
=
2
. Substitute into y’s equation to get
y
x
y
x
= − =
−
2
1
2
2
or
.
© 2010 e College Board.
12
Vectors
7.
2
1
and x t y
t
= =
t
–2 –1
−
1
2
0
1
2
1 2
x
–2 –1
−
1
2
0
1
2
1 2
y
1
4
1 4 und. 4 1
1
4
To eliminate the parameter, notice that t = x. Substitute into y’s equation to get
2
1
y
x
=
.
8.
x t y t= − = +2 1 3 1cos sin and
t
0
π
2
π
3
2
π
2
π
x
1 -1 -3 -1 1
y
1 4 1 -2 1
To eliminate the parameter, solve for cos t in x’s equation and sin t in y’s equation.
Substitute into the trigonometric identity
cos sin
2 2
1
t t
+ =
to get
x y+
( )
+
−
( )
=
1
4
1
9
1
2 2
.
© 2010 e College Board.
13
Vectors
9. x = 2sin t –1 and y = cos t + 2
t
0
π
2
π
3
4
π
2
π
x
–1 1 –1 –3 –1
y
3 2 1 2 3
To eliminate the parameter, solve for cos t in y’s equation and sin t in x’s equation.
Substitute into the trigonometric identity cos
2
t + sin
2
t = 1 to get
x
y
+
( )
+ −
( )
=
1
4
2 1
2
2
.
10.
x = sec t and y = tan t
t
0
π
4
π
2
3
4
π
π
5
4
π
3
2
π
7
4
π
2
π
x
1
2
und.
− 2
–1
− 2
und.
2
1
y
0 1 und. –1 0 1 und. –1 0
To eliminate the parameter, substitute into the trigonometric identity 1 + tan
2
t =
sec
2
t to get 1 + y
2
= x
2
or x
2
– y
2
= 1.
© 2010 e College Board.
14
Vectors
Day 2: Parametric Equations
and Calculus
If your textbook contains this material, you might want to follow your book here.
Formulas to Know
If a smooth curve C is given by the equations x = f(t) and y = g(t), then the slope of C at
the point (x, y) is given by
dy
dx
dy
dt
dx
dt
dx
dt
= ≠, where 0
, and the second derivative is given by
d y
dx
d
dx
dy
dx
d
dt
dy
dx
dx
dt
2
2
=
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
.
e reason that
dy
dx
dy
dt
dx
dt
dx
dt
= ≠, where 0
, is the Chain Rule:
Since y is a function of x, and x is a function of t, the Chain Rule gives
dy
dt
dy
dx
dx
dt
= ⋅
,
hence
dy
dx
dy
dt
dx
dt
dx
dt
= ≠, where 0
. Applying this formula to
dy
dx
and x rather than to y and
x, we have
d y
dx
d
dx
dy
dx
d
dt
dy
dx
dx
dt
2
2
=
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
.
Or, applying the Chain Rule: Since
dy
dx
is a function of x, and x is a function of t,
we have
d
dt
dy
dx
d
dx
dy
dx
dx
dt
d y
dx
dx
dt
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
⋅ = ⋅
2
2
, hence
d y
dx
d
dt
dy
dx
dx
dt
2
2
=
⎡
⎣
⎢
⎤
⎦
⎥
.
© 2010 e College Board.
15
Vectors
Example 1 (no calculator): Given the parametric equations
x t y t t= = −2 3 2
2
and
, nd
dy
dx
d y
dx
and
2
2
.
Solution:
To nd
dy
dx
, we must dierentiate both of the parametric equations with respect to t.
Since
dy
dt
d
dt
t t t
dx
dt
d
dt
t= −
⎡
⎣
⎤
⎦
= − =
⎡
⎣
⎤
⎦
= ⋅3 2 6 2 2 2
2
and
11
2
1
2
1
2
t t
− −
=
, then
dy
dx
dy
dt
dx
dt
t
t
t t= =
−
= −
−
6 2
6 2
1
2
3
2
1
2
.
To nd
d y
dx
2
2
, we must dierentiate
dy
dx
with respect to t and divide by
dx
dt
:
d y
dx
d
dt
dy
dx
dx
dt
d
dt
t t
dx
dt
2
2
6 2
3
2
1
2
=
⎡
⎣
⎢
⎤
⎦
⎥
=
−
⎡
⎣
⎢
⎤
⎦
⎥
==
−
=
−
= −
− −
−
9 9
9 1
1
2
1
2
1
2
1
2
1
2
t t
dx
dt
t t
t
t
.
Example 2 (no calculator): Given the parametric equations x = 4cos t and y = 3 sin t, write
an equation of the tangent line to the curve at the point where
t =
3
4
π
.
Solution:
dy
dx
dy
dt
dx
dt
d
dt
t
d
dt
t
t
= =
⎡
⎣
⎤
⎦
⎡
⎣
⎤
⎦
=
−
3
4
3
4
sin
cos
cos
s
iin
cot
t
t= −
3
4
.
When andt
dy
dx
x y= = − −
( )
= = −
⎛
⎝
⎜
⎞
⎠
⎟
= − =
3
4
3
4
1
3
4
4
2
2
2 2
π
, , 33
2
2
3 2
2
⎛
⎝
⎜
⎞
⎠
⎟
=
.
erefore the tangent line equation is:
y x− = +
( )
3 2
2
3
4
2 2
.
(Remind students that they may leave their tangent line equations in point-slope form.)

© 2010 e College Board.
16
Vectors
Example 3 (no calculator): Find all points of horizontal and vertical tangency given the
parametric equations
x t t y t t= + = − +
2 2
3 5, .
Solution:
dy
dx
dy
dt
dx
dt
d
dt
t t
d
dt
t t
t
t
= =
− +
⎡
⎣
⎤
⎦
+
⎡
⎣
⎤
⎦
=
−
+
2
2
3 5
2 3
2
11
.
A horizontal tangent will occur when
dy
dx
= 0
, which happens when 2t – 3 = 0
(and 2t + 1 ≠ 0 ), so a horizontal tangent occurs at t =
3
so a horizontal tangent occurs at
2
t =
. Substituting
3
2
t =
into the given
equations, we nd that a horizontal tangent will occur at
15
4
11
4
,
⎛
⎝
⎜
⎞
⎠
⎟
. A vertical tangent
will occur when
dy
dx
is undened, which happens when 2t + 1 = 0 (and 2t – 3 ≠ 0), so a
vertical tangent occurs at
t = −
1
2
. Substituting
t = −
1
2
into the given equations, we nd
that a vertical tangent will occur at
−
⎛
⎝
⎜
⎞
⎠
⎟
1
4
27
4
,
.
Example 4 (no calculator): Set up an integral expression for the arc length of the curve
given by the parametric equations x = t
2
+ 1, y = 4t
3
– 1, 0 ≤ t ≤ 1. Do not evaluate.
Solution:
For parametric equations x = f(t) and y = g(t), a ≤ t ≤ b, the formula for arc length is:
s
dx
dt
dy
dt
dt
a
b
=
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
∫
2 2
.
For our problem,
dx
dt
d
dt
t t
dy
dt
d
dt
t t= +
⎡
⎣
⎤
⎦
= = −
⎡
⎣
⎤
⎦
=
2 3 2
1 2 4 1 12 and
, so the arc
length is given by the integral expression
s t t dt t t dt=
( )
+
( )
= +
∫ ∫
2 12 4 144
2
2
2 4
2
0
1
0
1
.
© 2010 e College Board.
17
Vectors
Day 2 Homework
Do not use your calculator on the following problems.
On problems 1–5, nd
dy
dx
d y
dx
and
2
2
.
1.
x t y t t= = + +
2 2
6 5,
2.
x t y t t= + = −
2 3 2
1 2,
3.
x t y t t= = +, 3 2
2
4.
x t y t t
= = +ln ,
2
5.
x t y t= + = −3 2 4 1sin , cos
6. A curve C is dened by the parametric equations
x t t y t t= + − = −
2 3 2
1,
. Find:
(a)
dy
dx
in terms of t.
(b) an equation of the tangent line to C at the point where t = 2.
7. A curve C is dened by the parametric equations
x t y t= =2 3cos , sin
. Find:
(a)
dy
dx
in terms of t.
(b) an equation of the tangent line to C at the point where t =
π
4
.
On problems 8–10, nd:
(a)
dy
dx
in terms of t.
(b) all points of horizontal and vertical tangency.
8.
x t y t t= + = −5 4
2
,
9.
x t t y t t= − + = −
2 3
1 3,
10.
x t y t= + = − +3 2 1 4cos , sin
,
0 2≤ <t
π
On problems 11–12, a curve C is dened by the parametric equations given. For
each problem, write an integral expression that represents the length of the arc of the
curve over the given interval.
11.
x t y t t= = ≤ ≤
2 3
0 2, ,
12.
x e y t t
t
= + = − − ≤ ≤
2
1 3 1 2 2, ,

© 2010 e College Board.
18
Vectors
Answers to Day 2 Homework
1. Since
dy
dt
d
dt
t t t
dx
dt
d
dt
t= + +
⎡
⎣
⎤
⎦
= + =
⎡
⎣
⎤
⎦
=
2 2
6 5 2 6 2 and tt
,
then
dy
dx
dy
dt
dx
dt
t
t t
= =
+
= +
2 6
2
1
3
.
To nd
d y
dx
2
2
, we must dierentiate
dy
dx
with respect to t and divide by
dx
dt
:
d y
dx
d
dt
dy
dx
dx
dt
d
dt t
dx
dt
t
2
2
1
3
3
2
=
⎡
⎣
⎢
⎤
⎦
⎥
=
+
⎡
⎣
⎢
⎤
⎦
⎥
=
−
ddx
dt
t
t
t
=
−
= −
3
2
3
2
2
3
2.
2 2 6 2 1
3 2 2 2
.
dy
dt
d
dt
t t t t
dx
dt
d
dt
t= −
⎡
⎣
⎤
⎦
= − = +
⎡
and
⎣⎣
⎤
⎦
=
= =
−
= −
=
2
6 2
2
3 1
2
2
2
t
dy
dx
dy
dt
dx
dt
t t
t
t
d y
dx
d
dt
dy
d
xx
dx
dt
d
dt
t
dx
dt
dx
dt
t
⎡
⎣
⎢
⎤
⎦
⎥
=
−
⎡
⎣
⎤
⎦
= =
3 1
3 3
2
3.
3 3 2 6 2
1
2
.
dy
dt
d
dt
t t t
dx
dt
d
dt
t= +
⎡
⎣
⎤
⎦
= + =
⎡
⎣
⎤
⎦
= and
22
6 2
1
2
12 4
1
2
1
2
3
2
1
2
2
2
t
dy
dx
dy
dt
dx
dt
t
t
t t
d y
dx
−
−
= =
+
= +
==
⎡
⎣
⎢
⎤
⎦
⎥
=
+
⎡
⎣
⎢
⎤
⎦
⎥
=
d
dt
dy
dx
dx
dt
d
dt
t t
dx
dt
t
12 4
18
3
2
1
2
11
2
1
2
1
2
1
2
1
2
2 18 2
1
2
36 4
+
=
+
= +
− −
−
t
dx
dt
t t
t
t

© 2010 e College Board.
19
Vectors
4.
4 2 1
1
2
. ln
dy
dt
d
dt
t t t
dx
dt
d
dt
t= +
⎡
⎣
⎤
⎦
= + =
⎡
⎣
⎤
⎦
= and
tt
dy
dx
dy
dt
dx
dt
t
t
t t
d y
dx
d
dt
dy
dx
= =
+
= +
=
⎡
⎣
⎢
⎤
⎦
2 1
1
2
2
2
2
⎥⎥
=
+
⎡
⎣
⎤
⎦
=
+
=
+
= +
dx
dt
d
dt
t t
dx
dt
t
dx
dt
t
t
t t
2
4 1 4 1
1
4
2
2
5.
5 4 1 4 3
. cos sin sin
dy
dt
d
dt
t t
dx
dt
d
dt
= −
⎡
⎣
⎤
⎦
= − = and
tt t
dy
dx
dy
dt
dx
dt
t
t
t
+
⎡
⎣
⎤
⎦
=
= =
−
= −
2 3
4
3
4
3
cos
sin
cos
tan
dd y
dx
d
dt
dy
dx
dx
dt
d
dt
t
dx
dt
2
2
4
3
=
⎡
⎣
⎢
⎤
⎦
⎥
=
−
⎡
⎣
⎢
⎤
⎦
⎥
=
tan
−−
=
−
= −
4
3
4
3
3
4
9
2 2
3
sec sec
cos
sec
t
dx
dt
t
t
t
6. (a)
dy
dx
t t
t
=
−
+
3 2
2 1
2
.
(b) When t = 2,
dy
dx
x y=
⋅ − ⋅
⋅ +
= = =
3 2 2 2
2 2 1
8
5
5 4
2
, and
, so the tangent line
equation is
y x− = −
( )
4
8
5
5
.
© 2010 e College Board.
20
Vectors
7. (a)
dy
dx
t
t
t=
−
= −
3
2
3
2
cos
sin
cot
.
(b) When
t =
π
4
,
dy
dx
x y= − = − = =
3
2 4
3
2
2
3 2
2
cot ,
π
and
, so the tangent line
equation is
y x− = − −
( )
3 2
2
3
2
2
.
8. (a)
dy
dx
t
=
−2 4
1
with
dy
dt
t= −2 4
and
dx
dt
= 1
.
(b) A horizontal tangent occurs when
dy
dt
dx
dt
= ≠0 0 and
, so a horizontal tangent
occurs when 2t – 4 = 0, or at t = 2. When t = 2, x = 7 and y = –4, so a
horizontal tangent occurs at the point (7, –4). A vertical tangent occurs when
dx
dt
dy
dt
= ≠0 0 and
.
Since 1 ≠ 0, there is no point of vertical tangency on this curve.
9. (a)
dy
dx
t
t
=
−
−
3 3
2 1
2
with
dy
dt
t= −3 3
2
and
dx
dt
t= −2 1
.
(b) A horizontal tangent occurs when
dx
dt
dy
dt
= ≠0 0 and
, so a horizontal tangent
occurs when 3t
2
– 3 = 0, or when t = ±1. When t = 1, x = 1 and y = –2, and
when t = –1, x = 3 and y = 2, so horizontal tangents occur at the points (1, –2)
and (3, 2).
A vertical tangent occurs when
dx
dt
dy
dt
= ≠0 0 and
so a vertical tangent occurs
when
2 1 0
1
2
t t− = =, or
. When
t =
1
2
,
x y= = −
3
4
11
8
and
, so a vertical
tangent occurs at the point
3
4
11
8
, −
⎛
⎝
⎜
⎞
⎠
⎟
.
© 2010 e College Board.
21
Vectors
10. (a)
dy
dx
t
t
t=
−
= −
4
2
2
cos
sin
cot
with
dy
dt
t= 4cos
and
dx
dt
t= −2sin
.
(b) A horizontal tangent occurs when
dy
dt
dx
dt
= ≠0 0 and
, so a horizontal tangent
occurs when
4 0cos t =
, or at
t t= =
π π
2
3
2
and
. When t =
π
2
, x = 3 and y = 3,
and when
t =
3
2
π
, x = 3 and y = –5, so horizontal tangents occur at the points
3 3 3 5, ,
( )
−
( )
and
.
A vertical tangent occurs when
dx
dt
dy
dt
= ≠0 0 and
, so a vertical tangent
occurs when
− = = =2 0 0sin ,t t tor when and
π
. When
t = 0,
x y= = −5 1 and
, and when
t x y= = = −
π
, 1 1 and
, so vertical tangents
occur at the points
5 1 1 1, ,−
( )
−
( )
and
.
11.
s
dx
dt
dy
dt
dt t t dt
a
b
=
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
=
( )
+
( )
∫
2 2
2
2
2 3
2
0
2
∫∫ ∫
= +4 9
2 4
0
2
t t dt
.
12.
s
dx
dt
dy
dt
dt e dt
a
b
t
=
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
=
( )
+
( )
∫
−
2 2
2
2
2 3
2
2
22
4
2
4 9
2
∫ ∫
= +
−
e dt
t
.

© 2010 e College Board.
22
Vectors
Day 3: Review of Motion Along a Line
My students study motion along a line early in the year, so this assignment is a review
for them. I like to spend a day on motion along a line as a segue into motion along a
curve. For an excellent introduction to motion along a line, see the Curriculum Module
on motion by Dixie Ross at AP Central®. (http://apcentral.collegeboard.com/apc/public/
repository/AP_CurricModCalculusMotion.pdf)
Day 3 Homework
e following problems are from old AP Exams and the sample multiple-choice problems
in the Course Description, available at AP Central
(http://apcentral.collegeboard.com/apc/public/courses/teachers_corner/2118.html).
Multiple-Choice Items:
1. 2003 AP Calculus AB Exam, Item 25 (no calculator):
A particle moves along the x-axis so that at time
t ≥ 0
its position is given by
x t t t t
( )
= − + −2 21 72 53
3 2
.
At what time t is the particle at rest?
(A) t = 1 only
(B) t = 3 only
(C)
t =
7
2
only
(D) t = 3 and
t =
7
2
(E) t = 3 and t = 4
2. 1998 AP Calculus AB Exam, Item 24 (no calculator):
e maximum acceleration attained on the interval
0 3≤ ≤t
by the particle whose
velocity is given by
v t t t t
( )
= − + +
3 2
3 12 4
is
(A) 9
(B) 12
(C) 14
(D) 21
(E) 40

© 2010 e College Board.
23
Vectors
3. AP Calculus AB, sample multiple-choice Item 9 (no calculator):
e position of a particle moving along a line is given by
s t t t t t
( )
= − + + ≥2 24 90 7 0
3 2
for
.
For what values of t is the speed of the particle increasing?
(A) 3 < t < 4 only
(B) t > 4 only
(C) t > 5 only
(D) 0 < t < 3 and t > 5
(E) 3 < t < 4 and t > 5
4. 2003 AP Calculus AB Exam, Item 76 (calculator):
A particle moves along the x-axis so that at any time
t ≥ 0
, its velocity is given by
v t t
( )
= +3 4 1 0 9. cos( . )
. What is the acceleration of the particle at time t = 4?
(A) –2.016
(B) –0.677
(C) 1.633
(D) 1.814
(E) 2.97
5. 2003 AP Calculus AB Exam, Item 91 (calculator):
A particle moves along the x-axis so that at any time t > 0, its acceleration is
given by
a t
t
( )
= +
( )
ln .1 2
If the velocity of the particle is 2 at time t = 1, then the
velocity of the particle at time t = 2 is
(A) 0.462
(B) 1.609
(C) 2.555
(D) 2.886
(E) 3.346

© 2010 e College Board.
24
Vectors
6. AP Calculus AB, sample multiple-choice Item 19 (calculator):
Two particles start at the origin and move along the x-axis. For
0 10≤ ≤t
, their
respective position functions are given by
x t x e
t
1 2
2
1= = −
−
sin and
. For how
many values of t do the particles have the same velocity?
(A) None
(B) One
(C) Two
(D) ree
(E) Four
7. AP Calculus AB, sample multiple-choice Item 15 (calculator):
A particle travels along a straight line with a velocity of
v t e t
t
( )
=
( )
−
( )
3 2
2
sin
meters per second. What is the total distance traveled by the particle during the
time interval
0 2≤ ≤t
seconds?
(A) 0.835
(B) 1.850
(C) 2.055
(D) 2.261
(E) 7.025
Free-Response Questions:
8. 2004 AP Calculus AB Exam, FRQ 3 (calculator):
A particle moves along the y-axis so that its velocity at time
t ≥ 0
is given by
v t e
t
( )
= −
( )
−
1
1
tan
. At time t = 0, the particle is at y = –1. (Note:
tan arctan
−
=
1
x x
.)
(a) Find the acceleration of the particle at time t = 2.
(b) Is the speed of the particle increasing or decreasing at time t = 2? Give a reason
for your answer.
(c) Find the time
t ≥ 0
at which the particle reaches its highest point. Justify your
answer.
(d) Find the position of the particle at time t = 2. Is the particle moving toward the
origin or away from the origin at time t = 2? Justify your answer.
© 2010 e College Board.
25
Vectors
9. 2006 AP Calculus AB/BC Exams, Item 4 (no calculator):
t (seconds) 0 10 20 30 40 50 60 70 80
v(t) (feet per second) 5 14 22 29 35 40 44 47 49
Rocket A has positive velocity
v t
( )
aer being launched upward from an initial
height of 0 feet at time t = 0 seconds. e velocity of the rocket is recorded for
selected values of t over the interval
0 80≤ ≤t
seconds, as shown in the table
above.
(a) Find the average acceleration of rocket A over the time interval
0 80≤ ≤t
seconds. Indicate units of measure.
(b) Using correct units, explain the meaning of
v t dt
( )
∫
10
70
in terms of the rocket’s
ight. Use a midpoint Riemann sum with 3 subintervals of equal length to
approximate
v t dt
( )
∫
10
70
.
(c) Rocket B is launched upward with an acceleration of
a t
t
( )
=
+
3
1
feet per
second. At time t = 0 seconds, the initial height of the rocket is 0 feet, and the
initial velocity is 2 feet per second. Which of the two rockets is traveling faster
at time t = 80 seconds? Explain your answer.
Answers to Day 3 Homework
1. Since x'(t) = 6t
2
- 42t + 72 = 6(t
2
– 7t + 12) = 6(t – 3)(t – 4) = 0 when t = 3 and
when t = 4, the answer is E.
2. Note that a(t) = 3t
2
– 6t + 12, so that a'(t) = 6t – 6 = 0 when t = 1.
Computing the
acceleration at the critical number and at the endpoints of the interval, we have
a(0) = 12, a(1) = 9, and a(3) = 21. e maximum acceleration is 21, so the answer
is D.
3. Note that v(t) = 6t
2
– 48t + 90 = 6(t – 3)(t – 5) and a(t) = 12t – 48 = 12(t – 4).
e speed is increasing on 3 < t < 4, where the velocity and the acceleration are
both negative, and also for t > 5, where the velocity and the acceleration are both
positive, so the answer is E.
4. Since
d
dt
t
t
3 4 1 0 9 1 633
4
+
( )
⎡
⎣
⎤
⎦
=
−
. cos . .
, the answer is C.
5. Since
v dt
t
2 2 1 2 3 346
1
2
( )
= + +
( )
=
∫
ln .
, the answer is E.
© 2010 e College Board.
26
Vectors
6. First nd
d
dt
t t
d
dt
e e
t t
sin cos
⎡
⎣
⎤
⎦
=
⎡
⎣
⎤
⎦
= −
− −
and
2 2
2
. en graph y
1
= cos x and y
2
=
–2e
–2x
in function mode with an x-window of [0, 10] and a y- window of [–1 , 1].
e two graphs intersect at three points, so the answer is D.
7. Distance =
v t dt e t dt
t
( )
=
( )
=
∫ ∫
−
( )
0
2
0
2
2
3 2 2 261sin .
, so the answer is D.
8. (a) a(2) = v'(2) = –0.132 or –0.133.
(b) v(2) = – 0.436. Since a(2) < 0, and v(2) < 0, the speed is increasing.
(c) Note that v(t) = 0 when tan
–1
(e
t
) = 1. e only critical number for
y is t = ln(tan1) = 0.443. Since v(t) > 0 for 0 ≤ t < ln(tan 1) and
v(t) < 0 for t > ln(tan1), y(t) has an absolute maximum at t = 0.443.
(d)
y v t dt2 1 1 360 1 361
0
2
( )
= − +
( )
= − −
∫
. .or
.
Since v(2) < 0 and y(2) < 0, the particle is moving away from the origin.
9. (a) Average acceleration of rocket A is
v v80 0
80 0
49 5
80
11
20
2
( )
−
( )
−
=
−
= ft / sec
.
(b) Since the velocity is positive,
v t dt
( )
∫
10
70
represents the distance, in feet, traveled
by rocket A from t = 10 seconds to t = 70 seconds. A midpoint Riemann sum is
20 20 40 60 20 22 35 44 2020v v v
( )
+
( )
+
( )
⎡
⎣
⎤
⎦
= + +
( )
= ft
.
(c) Let
v t
B
( )
be the velocity of rocket B at time t. en
v t
t
dt t C
B
( )
=
+
= + +
∫
3
1
6 1
. Since
2 0 6=
( )
= +v C
B
, then C = – 4 and
v t t
B
( )
= + −6 1 4
. Hence,
v v
B
80 50 49 80
( )
= > =
( )
and Rocket B is
traveling faster at time t = 80 seconds.

© 2010 e College Board.
27
Vectors
Day 4: Motion Along a Curve —
Vectors
I give my students the following list of terms and formulas to know.
Parametric Equations, Vectors, and Calculus —
Terms and Formulas to Know:
If a smooth curve C is given by the equations
x f t y g t=
( )
=
( )
and ,
then the slope of C
at the point (x, y) is given by
dy
dx
dy
dt
dx
dt
dx
dt
= ≠ where 0
, and the second derivative is given
by
d y
dx
d
dx
dy
dx
d
dt
dy
dx
dx
dt
2
2
=
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
.
e derivative
dy
dx
also may be interpreted as the slope of the tangent line to the
curve C, or as the slope of the path of a particle traveling along the curve C, or as the rate
of change of y with respect to x.
e second derivative
d y
dx
2
2
is the rate of change of the slope of the curve C with
respect to x.
′
( )
=x t
dx
dt
is the rate at which the x-coordinate is changing with respect to t or the
velocity of the particle in the horizontal direction.
′
( )
=y t
dy
dt
is the rate at which the y-coordinate is changing with respect to t or the
velocity of the particle in the vertical direction.
© 2010 e College Board.
28
Vectors
x t y t
( ) ( )
,
is the position vector at any time t.
′
( )
′
( )
x t y t,
is the velocity vector at any time t.
′′
( )
′′
( )
x t y t,
is the acceleration vector at any time t.
dx
dt
dy
dt
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
2 2
is the speed of the particle or the magnitude (length) of the
velocity vector.
dx
dt
dy
dt
a
b
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
∫
2 2
dt is the length of the arc (or arc length) of the curve from
t a t b= = to
or the distance traveled by the particle from
t a t b= = to .
Most textbooks do not contain the types of problems on vectors that are found on
the AP Exam, so I supplement with the examples and worksheets below.
Example 1 (no calculator):
A particle moves in the xy-plane so that at any time t, the position of the particle is given
by
x t t t y t t t
( )
= +
( )
= −
3 2 3
4
4
, .
(a) Find the velocity vector when t = 1.
Solution:
v t
dx
dt
dy
dt
d
dt
t t
d
dt
t t t t t
( )
= = +
( )
−
( )
= +, , ,
3 2 4 3 2
4 3 8 4
33 2
3
1 11 1
−
( )
=
t
v ,
(b) Find the acceleration vector when t = 2.
Solution:
a t
d
dt
dx
dt
d
dt
dy
dt
d
dt
t t
d
d
( )
=
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
= +
( )
, ,3 8
2
tt
t t t t t
a
4 3 6 8 12 6
2 20 36
3 2 2
−
( )
= + −
( )
=
,
,
Example 2 (no calculator):
A particle moves in the xy-plane so that at any time t,
t ≥ 0
, the position of the particle is
given by
x t t t y t t t
( )
= +
( )
= −
2 3 2
3 3, .
Find the magnitude of the velocity vector when t = 1.
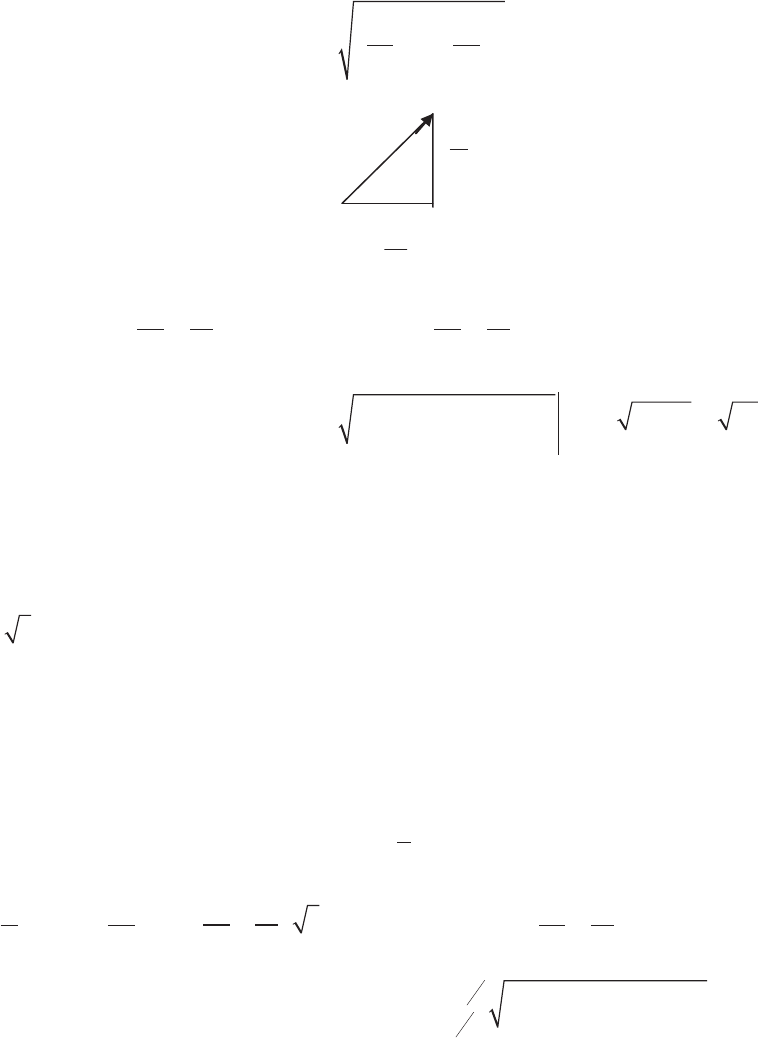
© 2010 e College Board.
29
Vectors
Solution:
e magnitude or length of the velocity vector can be found by using the Pythagorean
eorem, since the horizontal and vertical components make a right triangle, with the
vector itself as the hypotenuse. erefore its length is given by:
Magnitude of velocity vector =
dx
dt
dy
dt
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
2 2
Figure 15
dy
dt
dx
dt
For our problem,
dx
dt
d
dt
t t t= +
⎡
⎣
⎤
⎦
= +
2
3 2 3
and
dy
dt
d
dt
t t t t= −
⎡
⎣
⎤
⎦
= −
3 2 2
3 3 6
.
Magnitude of velocity vector =
2 3 3 6
2
2
1
2
t t t
t
+
( )
+ −
( )
=
=
25 9 34+ =
.
Notice that the formula for the magnitude of the velocity vector is the same as the formula for
the speed of the vector, which makes sense since speed is the magnitude of velocity.
Example 3 (no calculator):
A particle moves in the xy-plane so that
x t y t t= − = − ≤ ≤3 4 1 2 0 2cos sin , . and where
π
e path of the particle intersects the x-axis twice. Write an expression that
represents the distance traveled by the particle between the two x-intercepts. Do not evaluate.
Solution:
e path of the particle intersects the x-axis at the points where the y-component is equal
to zero. Note that
1 2 0
1
2
− = =sin sint t when
. For
0 2≤ ≤t
π
, this will occur when
t t= =
π π
6
5
6
and
. Since
dx
dt
d
dt
t t= −
⎡
⎣
⎤
⎦
=3 4 4cos sin
and
dy
dt
d
dt
t t= −
⎡
⎣
⎤
⎦
= −1 2 2sin cos
,
the distance traveled by the particle is Distance =
4 2
2 2
6
5
6
sin cost t dt
( )
+ −
( )
∫
π
π
.
© 2010 e College Board.
30
Vectors
Day 4 Homework
Use your calculator on problems 10 and 13c only.
1. If
x t y e
dy
dx
t
= − =
2
1
3
and find , .
2. If a particle moves in the xy-plane so that at any time t > 0, its position vector is
ln ,t t t
2 2
5 3+
( )
, nd its velocity vector at time t = 2.
3. A particle moves in the xy-plane so that at any time t, its coordinates are given by
x t y t t= − = −
5 4 3
1 3 2 and .
Find its acceleration vector at t = 1.
4. If a particle moves in the xy-plane so that at time t its position vector is
sin , ,3
2
3
2
t t−
⎛
⎝
⎜
⎞
⎠
⎟
π
nd the velocity vector at time
t =
π
2
.
5. A particle moves on the curve
y x= ln
so that its x-component has derivative
′
( )
= + ≥x t t t1 0 for .
At time t = 0, the particle is at the point (1, 0). Find
the position of the particle at time t = 1.
6. A particle moves in the xy-plane in such a way that its velocity vector is
1
3
+ t t, .
If the position vector at t = 0 is
5 0,
, nd the position of
the particle at t = 2.
7. A particle moves along the curve
xy x
dy
dt
= = =10 2 3. ,
If and what is the value off
dx
dt
what is the value of
xy x
dy
dt
= = =10 2 3. , If and what is the value off
dx
dt
?
8. e position of a particle moving in the xy-plane is given by the parametric
equations
x t t t y t t t= − − + = − + +
3 2 3 2
3
2
18 5 6 9 4 and .
For what value(s) of
t is the particle at rest?
9. A curve C is dened by the parametric equations
x t y t t= = − +
3 2
5 2 and .
Write
the equation of the line tangent to the graph of C at the point (8, –4).
10. A particle moves in the xy-plane so that the position of the particle is given by
x t t t y t t t
( )
= +
( )
= −
( )
−
( )
5 3 8 1sin cos . and
Find the velocity vector at the time
when the particle’s horizontal position is x = 25.
11. e position of a particle at any time
t ≥ 0
is given by
x t t y t t
( )
= −
( )
=
2 3
3
2
3
and .
(a) Find the magnitude of the velocity vector at time t = 5.
© 2010 e College Board.
31
Vectors
(b) Find the total distance traveled by the particle from t = 0 to t = 5.
(c) Find
dy
dx
as a function of x.
12. Point
P x y,
( )
moves in the xy-plane in such a way that
dx
dt t
dy
dt
t t
=
+
= ≥
1
1
2 0 and for .
dx
dt t
dy
dt
t t
=
+
= ≥
1
1
2 0
and for .
(a) Find the coordinates of P in terms of t given that, when t = 1,
x = ln 2
and y = 0.
(b) Write an equation expressing y in terms of x.
(c) Find the average rate of change of y with respect to x as t varies from 0 to 4.
(d) Find the instantaneous rate of change of y with respect to x when t = 1.
13. Consider the curve C given by the parametric equations
x t= −2 3cos
and
y t= +3 2sin
, for
− ≤ ≤
π π
2 2
t
.
(a) Find
dy
dx
as a function of t.
(b) Find the equation of the tangent line at the point where
t =
π
4
.
(c) e curve C intersects the y-axis twice. Approximate the length of the curve
between the two y-intercepts.
Answers to Day 4 Homework
1.
dy
dx
dy
dt
dx
dt
d
dt
e
d
dt
t
t e
t
t
t
t
= =
⎡
⎣
⎤
⎦
−
⎡
⎣
⎤
⎦
= =
3
3
2
2
1
3
2
3
ee
t
3
2
.
2.
v t
dx
dt
dy
dt
t
t t
t v
( )
= =
+
+
( )
=, , ,
2 5
5
6 2
9
14
12
2
so
.
3.
v t
dx
dt
dy
dt
t t t
( )
= = −, ,5 12 6
4 3 2
.
a t
d x
dt
d y
dt
t t t
( )
= = −
( )
=
2
2
2
2
20 36 12 20 24
3 2
, , ,, so a 1
.
4.
v t
dx
dt
dy
dt
t t v
( )
= = −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
, cos ,3 3
2
6
2
π π
so == = −3 3 3 3cos , ,
π π π
.
© 2010 e College Board.
32
Vectors
5.
x t t dt
t
t C
( )
= +
( )
= + +
∫
1
2
2
.
x C x t
t
t0 1
2
1
2
( )
= =
( )
= + + so
.
Since
x y1
5
2
1
5
2
5
2
5
2
( )
=
( )
=
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
⎝
and Position ln , , ln
⎜⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎞
⎠
⎟
.
Or, since
x t dt y1 1 1
5
2
1
5
2
0
1
( )
= + +
( )
=
( )
=
⎛
⎝
⎜
⎞
⎠
⎟
∫
and Positln , iion =
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
5
2
5
2
, ln
.
6.
x t t dt t
t
C x C x t
( )
= +
( )
= + +
( )
= =
( )
=
∫
1
2
0 5 5
2
. so and tt
t
+ +
2
2
5
.
y t t dt
t
D y D y t
t
( )
= = +
( )
= =
( )
=
∫
3
4 4
4
0 0 0
4
. .so and
Po
ssition vector At Position= + + = =t
t t
t
2 4
2
5
4
2 9 4, . , ,
(( )
( )
= + +
( )
=
( )
= +
∫
.
Or, since and x t dt y t d2 5 1 9 2 0
0
2
3
tt
0
2
4
9 4
∫
=
=
( )
,
, .Position
7. When x = 2, y = 5.
x
dy
dt
y
dx
dt
dx
dt
dx
dt
+ =
( )( )
+ = = −
0
2 3 5 0
6
5
so
Or nd that
dy
dx
x
= −
10
2
. en substituting into
dy
dx
dy
dt
dx
dt
=
gives
−
=
10
4
3
dx
dt
so that
dx
dt
= −
6
5
.
8.
′
( )
= − − = −
( )
+
( )
= = = −x t t t t t t t3 3 18 3 3 2 0 3
2
when and 22
.
′
( )
= − + = −
( )
−
( )
= = =y t t t t t t t3 12 9 3 1 3 0 3 1
2
when and ..
,The particle is at rest when so at rev t
( )
= 0 0 sst when t = 3.
© 2010 e College Board.
33
Vectors
9.
9 8 5 2 4
2 5 6 0
3 2 0
3 2
3 2
2
.
,
t t t
t t t
t t
t t
= − + = −
= − + =
−
( )
−
( )
=
= =
AAt when
Tange
8 4 2
2 5
3
1
12
2
2
2
, −
( )
=
=
−
= =
= −
t
dy
dx
t
t
t t
nnt line equation: y x+ = − −
( )
4
1
12
8
10.
10 5 3 25 5 445755. sin . ...
,
t t t
v t
dx
dt
dy
d
+ = =
( )
=
when
tt
t t t t
v
= + − + + −
( )
( )
=
5 3 1 8
5 445755 7 00
cos , cos sin
. ... . 88 2 228, .−
11. (a)
Magnitude when is or t t t
t
=
( )
+
( )
=
=5 2 2 2600
2
2
2
5
10 26
(b)
Distance =
( )
+
( )
= + = +
( )
∫
2 2 2 1
2
3
1
2
2
2
0
5
2 2
3
t t dt t t dt t
22
3
2
0
5
0
5
2
3
26 1
∫
= −
⎛
⎝
⎜
⎞
⎠
⎟
(c)
dy
dx
t
t
t x= = = +
2
2
3
2
© 2010 e College Board.
34
Vectors
12. (a)
x t
t
dt t C t x C
( )
=
+
= +
( )
+ = = =
∫
1
1
1 1 2 0ln . , ln .When so
xx t t
y t t dt t D t y
( )
= +
( )
( )
= = + = =
∫
ln
. ,
1
2 1 0
2
When so DD
y t t
x y t t
= −
( )
= −
( )
= +
( )
−
( )
1
1
1 1
2
2
.
, ln ,
(b)
t e t e y e e e
x x x x x
+ = = − = −
( )
− = −1 1 1 1 2
2
2
so and
.
(c)
Average rate of change =
( )
−
( )
( )
−
( )
=
( )
−
(
y b y a
x b x a
y y4 0
))
( )
−
( )
=
− −
( )
−
=
x x4 0
15 1
5 1
16
5ln ln ln
(d)
Instantaneous rate of change =
=
=
=
+
dy
dx
t
t
t
t
1
2
1
1
11
4=
13. (a)
dy
dx
t
t
t= =
2
3
2
3
cos
sin
cot
(b)
y x− +
( )
= − −
⎛
⎝
⎜
⎞
⎠
⎟
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
3 2
2
3
2
3 2
2
(c) x = 0 when
t = −0 84106867 0 84106867. ..., . ...
length =
3 2 3 756 3
2 2
0 841
0 841
sin cos . .
. ..
. ,,,
.
t t dt
( )
+
( )
=
−
∫
or 7757
© 2010 e College Board.
35
Vectors
Day 5: Motion Along a Curve —
Vectors (continued)
Example (calculator):
An object moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at time t
with
dx
dt
t
dy
dt
t=
( )
=
( )
sin , cos .
3 2
At time t = 2, the object is at the position (1, 4).
(a) Find the acceleration vector for the particle at t = 2.
(b) Write the equation of the tangent line to the curve at the point where t = 2.
(c) Find the speed of the vector at t = 2.
(d) Find the position of the particle at time t = 1.
Solution:
(a) Students should use their calculators to numerically dierentiate both
dx
dt
dy
dt
and
when t = 2 to get
a 2 1 476 3 027
( )
= − . , .
.
(b) When t = 2,
dy
dx
= −
cos
sin
.
4
8
0 661 or
, so the tangent line equation is
y x y x− = −
( )
− = − −
( )
4
4
8
1 4 0 661 1
cos
sin
. or
.
Notice that it is ne to leave the slope as the exact value or to write it as a decimal
correct to three decimal places.
(c) Speed =
dx
dt
dy
dt
⎛
⎝
⎜
⎞
⎠
⎟
+
⎛
⎝
⎜
⎞
⎠
⎟
2 2
=
sin cos .8 4 1 186
2 2
( )
+
( )
or
Notice that it is ne to leave the speed as the exact value or to write it as a
decimal correct to three decimal places.
(d) Students should apply the Fundamental eorem of Calculus to nd the x and y
components of the position.
x x x t dt y y y t dt
t
1 2 1 2
1
1
2
1
2
( )
=
( )
−
′
( ) ( )
=
( )
−
′
( )
= −
∫ ∫
sin
33
1
2
2
1
2
4
0 782 4 443
( )
= −
( )
= =
∫ ∫
dt t dtcos
. .
erefore the position at time t = 1 is (0.782, 4.443).
© 2010 e College Board.
36
Vectors
Day 5 Homework
Use your calculator on problems 7–11 only.
1. If
x e y t
dy
dx
t
= =
( )
2
3 and find sin ,
in terms of t.
2. Write an integral expression to represent the length of the path described by the
parametric equations
x t y t t= = ≤ ≤cos sin .
3 2
0
2
and for
π
3. For what value(s) of t does the curve given by the parametric equations
x t t y t t t= − − = + −
3 2 4 2
1 2 8 and
have a vertical tangent?
4. For any time
t ≥ 0
, if the position of a particle in the xy-plane is given by
x t y t= + = +
( )
2
1 2 3 and ln ,
nd the acceleration vector.
5. Find the equation of the tangent line to the curve given by the parametric
equations
x t t t y t t t
( )
= − +
( )
= −3 4 2 4
2 3
and
at the point on the curve
where t = 1.
6. If
x t e y e
t t
( )
= + =1 2
2
and
are the equations of the path of a particle moving in
the xy-plane, write an equation for the path of the particle in terms of x and y.
7. A particle moves in the xy-plane so that its position at any time t is given by
x t y t=
( )
=cos .5
3
and
What is the speed of the particle when t = 2?
8. e position of a particle at time
t ≥ 0
is given by the parametric equations
x t
t
y t t t
( )
=
−
( )
+
( )
= − +
2
3
4 4 4
3
2
and
.
(a) Find the magnitude of the velocity vector at t = 1.
(b) Find the total distance traveled by the particle from t = 0 to t = 1.
(c) When is the particle at rest? What is its position at that time?
9. An object moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at
time
t ≥ 0
with
dx
dt
t
dy
dt
e
t
= +
( )
=1 3
2
tan and
. Find the acceleration
vector and the speed of the object when t = 5.
10. A particle moves in the xy-plane so that the position of the particle is given by
x t t t y t t t t
( )
= +
( )
= + ≤ ≤cos sin , . and 3 2 0
π
Find the velocity vector when
the particle’s vertical position is y = 5.
© 2010 e College Board.
37
Vectors
11. An object moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at
time t with
dx
dt
t
dy
dt
t t=
( )
=
( )
≤ ≤2 0 4
3 2
sin cos . and for
At time t = 1, the
object is at the position (3, 4).
(a) Write an equation for the line tangent to the curve at (3, 4).
(b) Find the speed of the object at time t = 2.
(c) Find the total distance traveled by the object over the time interval
0 1≤ ≤t .
(d) Find the position of the object at time t = 2.
Answers to Day 5 Homework
1.
dy
dx
t
e
t
=
( )
3 3
2
2
cos
2. Length =
9 4
4 2 2 2
0
2
cos sin sin cost t t t dt+
∫
π
3.
dy
dx
t t
t t
t t=
+ −
−
− =
4 4 8
3 2
3 2 0
3
2
2
is undefined when
.
So the curve given by the parametric equations x = t
3
– t
2
– 1 and y = t
4
+2t
2
– 8t
has a vertical tangent when t = 0 and t =
2
3
.
4.
4 2
2
2 3
2
4
2 3
2
. , , ,
v t t
t
a t
t
( )
=
+
( )
= −
+
( )
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
5.
5
3 4
6 1
1
2
1 1 3
1
2
1
. , , .
dy
dx
t
t
t x y
t
t
=
=
=
−
−
= − = = = −. When
TTangent line equation: y x+ = − −
( )
3
1
2
1
6.
e x e x x y e y x x
t t t
= − = − + = = −1 2 1 2 2 4
2 22 2
so Then so . ++ 2.
7. Speed =
−
( )
( )
+
( )
=
5 5 3
2
2
2
2
sin t t
t
= 12.304
© 2010 e College Board.
38
Vectors
8. (a) Magnitude =
t t
t
−
( )
+ −
( )
=
=2 2 4
4 2
1
5
(b) Distance =
t t dt−
( )
+ −
( )
=
∫
2 2 4
4 2
0
1
3.816
(c) e particle is at rest when
v t t t
( )
= −
( )
− =2 2 4 0 0
2
, ,
, so is at rest when
t = 2. Position = (4, 0)
9.
a 5 10 178 6 277
( )
= . , .
, speed =
1 3
2
2
2
5
+
( )
( )
+
( )
=
tan t e
t
t
= 28.083
10.
10 3 2 5 1 079
1 079 0 119
. sin . ...
. ... .
t t t
v
+ = =
( )
=
when
,, .3 944
11.
11
2
0 321
2
3
1
. ( )
cos
sin
.a
Tangent line e
dy
dx
t
t
t
=
( )
( )
=
=
qquation: y x− = −
( )
4 0 321 3.
(b) Speed =
4
2 3 2 2
2
sin cost t
t
( )
+
( )
=
=
2.084
(c) Distance =
4
2 23 2
0
1
sin cost t dt
( )
+
( )
=
∫
1.126
( ) sin . , cosd x t dt y t2 3 2 3 436 2 4
3
1
2
2
1
2
( )
= +
( )
=
( )
= +
( )
∫ ∫
ddt = 3 557.
so position
= (3.436, 3.557)

© 2010 e College Board.
39
Vectors
Day 6: Motion Along a Curve —
Vectors (continued)
I don’t work any examples on Day 6. e students usually need a little more practice on
vectors, but no new material is covered in the Day 6 homework.
Day 6 Homework
Use your calculator only on problems 3–7.
1. e position of a particle at any time t ≥ 0 is given by
x t t y t t
( )
= −
( )
=
2 3
2
2
3
, .
(a) Find the magnitude of the velocity vector at t = 2.
(b) Set up an integral expression to nd the total distance traveled by the particle
from t = 0 to t = 4.
(c) Find
dy
dx
as a function of x.
(d) At what time t is the particle on the y-axis? Find the acceleration vector at this time.
2. An object moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at time t
with the velocity vector
v t
t
t
( )
=
+
⎛
⎝
⎜
⎞
⎠
⎟
1
1
2, .
At time t = 1, the object is at (ln 2, 4).
(a) Find the position vector.
(b) Write an equation for the line tangent to the curve when t = 1.
(c) Find the magnitude of the velocity vector when t = 1.
(d) At what time t > 0 does the line tangent to the particle at
x t y t
( ) ( )
( )
,
have a
slope of 12?
3. A particle moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
, with
x t t t y t t t t
( )
= +
( )
= + ≤ ≤2 3 2 0 10
2
sin cos , and where ..
Find the velocity vector
at the time when the particle’s vertical position is y = 7.
4. A particle moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at time t
with
dx
dt
t= +
( )
1
3
sin
. e derivative
dy
dt
is not explicitly given. For any time t, t
≥ 0, the line tangent to the curve at
x t y t
( ) ( )
( )
,
has a slope of t + 3. Find the
acceleration vector of the object at time t = 2.
© 2010 e College Board.
40
Vectors
5. An object moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at time
t with
dx
dt
e
dy
dt
e t
t t
=
( )
=
( )
≤ ≤cos sin . and for 0 2
At time t = 1, the object is at
the point (3, 2).
(a) Find the equation of the tangent line to the curve at the point where t = 1.
(b) Find the speed of the object at t = 1.
(c) Find the total distance traveled by the object over the time interval
0 2≤ ≤t .
(d) Find the position of the object at time t = 2.
6. A particle moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at time
t with
dx
dt
t t
dy
dt
t t= −
( )
= −
( )
sin cos .
3 3
and
At time t = 3, the particle is at the
point (1, 4).
(a) Find the acceleration vector for the particle at t = 3.
(b) Find the equation of the tangent line to the curve at the point where t = 3.
(c) Find the magnitude of the velocity vector at t = 3.
(d) Find the position of the particle at time t = 2.
7. An object moving along a curve in the xy-plane has position
x t y t
( ) ( )
( )
,
at time t
with
dy
dt
e
t
= +
( )
2 sin .
e derivative
dx
dt
is not explicitly given. At t = 3, the
object is at the point (4, 5).
(a) Find the y-coordinate of the position at time t = 1.
(b) At time t = 3, the value of
dy
dx
is
−1 8.
. Find the value of
dx
dt
when t = 3.
(c) Find the speed of the object at time t = 3.
© 2010 e College Board.
41
Vectors
Answers to Day 6 Homework
1. (a) Magnitude =
2 2
2
2
2
2
t t
t
( )
+
( )
=
=
4 5
(b) Distance =
4 4
2 4
0
4
t t dt+
∫
(c)
dy
dx
t
t
t x= = = +
2
2
2
2
(d) Particle is on the y-axis when
t = 2
, and
dx
dt
t= −2 1
2. (a)
x t
t
dt t C
( )
=
+
= +
( )
+
∫
1
1
1ln
. Since
x C1 2 0
( )
= =ln ,
.
y D1 4 3
( )
= =,
. Since
y D1 4 3
( )
= =,
.
Position vector ln t+1=
( )
+
( )
,t
2
3
(b) When t = 1,
dy
dx
= =
2
4
1
2
so the tangent line equation is
y x− = −
( )
4 4 2ln
.
(c) Magnitude =
1
1
2
17
2
2
2
1
t
t
t
+
⎛
⎝
⎜
⎞
⎠
⎟
+
( )
=
=
(d)
dy
dx
t
t
t t t t t=
+
= +
( )
= + − = =
2
1
1
2 1 12 2 2 12 0
2
when so 22
3.
t t t v
2
2 7 2 996 2 996 0 968 5+ = =
( )
= −cos . ... . ... . , when ..704
4.
dy
dt
dx
dt
t t t a=
⎛
⎝
⎜
⎞
⎠
⎟
+
( )
= +
( )
+
( ) ( )
= −3 1 3 2 1
3
so sin .. , .746 6 741−
5. (a) When t = 1,
dy
dx
e
e
t
t
t
=
( )
( )
= −
=
sin
cos
.
1
0 451 so the tangent linne equation is y x− = − −
( )
2 0 451 3.
(b) Speed =
cos sine e
t t
t
( )
( )
+
( )
( )
=
=
2 2
1
1
(c) Distance =
cos sine e dt
t t
( )
( )
+
( )
( )
=
∫
2 2
0
2
2
( ) cos . , sind x e dt y e d
t t
2 3 2 896 2 2
1
2
1
2
( )
= +
( )
=
( )
= +
( )
∫ ∫
tt = 1 676.
so position = (2.896, 1.676)

© 2010 e College Board.
42
Vectors
6. (a)
a 3 0
( )
= 11 29 23 545. , .
(b)
dy
dx
t t
t t
t
=
−
( )
−
( )
= −
=
cos
sin
.
3
3
3
0 468 so the tangentt line equation is y x− = − −
( )
4 0 468 1.
(c) Magnitude =
sin cost t t t
t
3 3
3
2 2
−
( )
( )
+ −
( )
( )
=
=
1
( ) sin . , cosd x t t dt y t t2 1 0 932 2 4
3
2
3
3
( )
= − −
( )
=
( )
= − −
( )
∫
22
3
4 002
∫
=dt .
so the
position = (0.932, 4.002)
7. (a)
y e dt
t
1 5 2
1
3
( )
= − +
( )
( )
=
∫
sin
1.269
(b)
dy
dx
e
dx
dt
dx
dt
e
t
t
=
+
( )
= − =
+
( )
−
=
2
1 8
2
3
3
sin
.
sin
so
11 8.
=
−1 636.
(c) Speed =
2
1 8
2
3
3
2
2
+
( )
−
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
+ +
( )
( )
=
sin
.
sin
e
e
3.368
© 2010 e College Board.
43
Vectors
About the Author
Nancy Stephenson teaches at Clements High School in Sugar Land, Texas. She was a
member of the AP Calculus Development Committee from 1999 to 2003 and is a College
Board consultant.
